Week 4 - Predicting Words

Week 4 - Links

4a - Learning To Predict The Next Word

Family Tree Example Intro

An alternative way to express family tree is to make a set of triples using 12 relationships connecting entities: son, daughter, nephew, niece, father, mother, uncle, aunt, brother, sister, husband, wife

(colin has-father james) & (colin has-mother victoria) → (james has-wife victoria)

(charlotte has-brother colin) & (victoria has-brother arthur) → (charlotte has-uncle arthur)

A relational learning task: given a large set of triples that come from some family trees, figure out the regularities.

Family Tree Neural Network Explanation

At the bottom left of the diagram that says "local encoding of person one" has twenty four neurons, and exactly one of those will be turned on for each training case.

At the bottom right of the diagram that says "local encoding of relationship," there are twelve relationships, and exactly one of the relationship units will be turned on.

At the top, there are twenty four output neurons, one for each person.

After the network has been trained, one feeds a person and a relationship type into the network, and hopefully gets out a correct person or no person.

4a Question

For the 24 people involved, the local encoding is created using a sparse 24-dimensional vector with all components zero, except one. E.g. Colin $\equiv(1,0,0,0,0,\ldots,0)$, Charlotte $\equiv(0,0,1,0,0,\ldots,0)$, Victoria $\equiv (0,0,0,0,1,\ldots,0)$ and so on.

Why don't we use a more succinct encoding like the ones computers use for representing numbers in binary? Colin $\equiv (0, 0, 0, 0, 1)$, Charlotte $\equiv (0, 0, 0, 1, 1)$, Victoria $\equiv (0, 0, 1, 0, 1)$ etc, even though this encoding will use 5-dimensional vectors as opposed to 24-dimensional ones. Check all that apply.

1. It's always better to have more input dimensions
2. The 24-d encoding makes each subset of persons linearly separable from every other disjoint subset while the 5-d does not
3. Considering the way this encoding is used, the 24-d encoding asserts no a-priori knowledge about the persons while the 5-d one does.

4a Question Work

1. False. Correct
2. True. I can picture how to make a perceptron partition subsets in the 24-d version of the problem, and it's harder to picture how that would work in the 5-d version as several people may share a bit. I'm not quite sure I can explain why or if the 5d version is completely not linearly separable or if it would just take a more complicated set of hidden units to separate it, though. Correct
3. True. It is true that the 5-d version encodes an "ordering", so there is an opportunity for some a-priori knowledge to leak in. Correct

Family Tree Network Design

A bottleneck is when there are fewer neurons than there are bits of data, so that the neuron is forced to learn interesting representations; there are 24 people but only six hidden units, so the system must learn to identify things about the people from other characteristics than whether or not their 1/24th of the vector is active.

In the bottleneck, it has to rerepresent those people as patterns of activity over those six neurons, with the hope that when it learns these propositions, the way in which it encodes a person will reveal structure in the domain.

We train it up on 112 propositions, and go through it many times, slowly changing the weights using backpropagation. Then we look at the weights in the six units in each of the distributed encoding layers right above the bottom layers. The resulting weights are shown in the grey boxes:

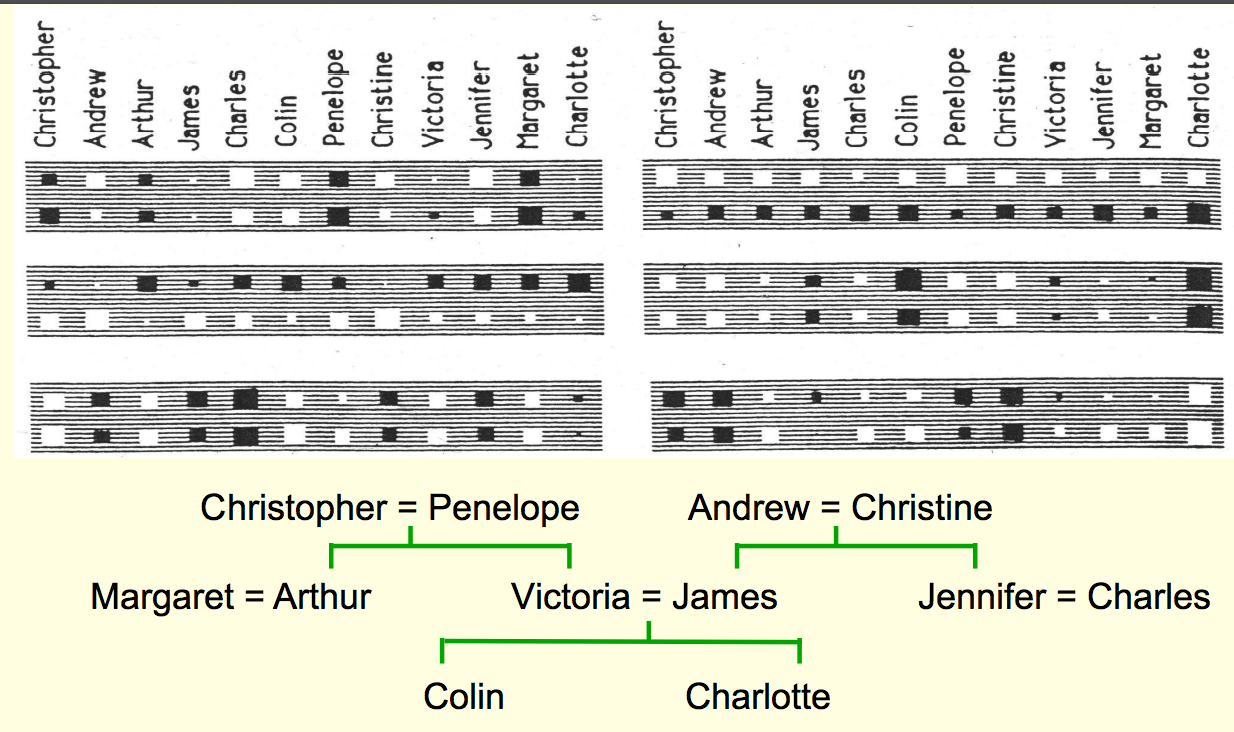
He laid out the twelve English people along a row "on the top and the Italian people on a row underneath."

Each of the six blocks is one of the six neurons encoding the people input layer. Each of these blocks has 24 blobs in it, and the blobs tell you the incoming weights for one of the people. He has arranged it so that within each neuron, the blobs on the top correspond to the English person and the blob on the bottom corresponds to the Italian equivalent.

If you go back to the slide "The structure of the neural net," look at the box "distributed encoding of person 1." There are six neurons there in that box and the boxes and blobs in the second slide is the incoming weights for each of those six neurons. These six hidden units form the bottleneck connected to the input representation of person 1 learn nationality, generation, branch of family tree.

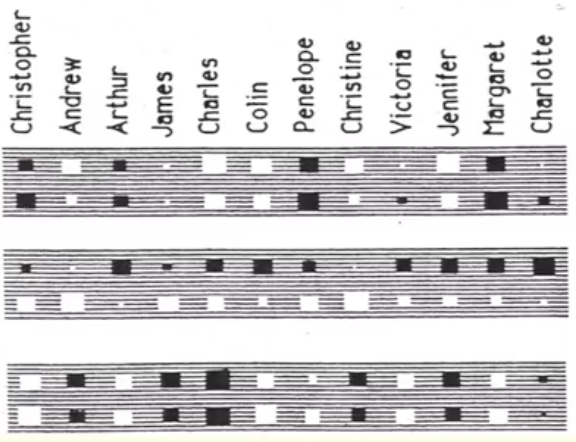
The diagram is a little confusing, because he's repeated the English names twice, but that's only because each English person has an Italian equivalent, and he wanted to represent the information in a horizontally compact form. A more realistic form would be like this:

Each column is both the English and the Italian. Each box is a neuron. The top row in the box is the data for the English person, the bottom row for the box is the data for the Italian.

If you look at the big grey rectangle on the top right (4th from top box above), you'll see that the weights along the top that come from English people are all positive, and the weights along the bottom are all negative. That means this neuron tells you whether the input person is English or Italian. We never gave the network that information explicitly, but it's useful information to have in this simple world, so the net learned it, because in the simple family trees that we've learned, if the input person is English, then the output person is always English. By encoding that information about each person it was able to halve the number of possibilities for that person.

These features are only useful if the other bottlenecks use similar representations and the central layer learns how features predict other features: (Input person is of generation 3) & (relationship requires answer to be one generation up) → (Output person is of generation 2)

If trained on eight of the relationship types, then tested on the remaining four, it gets answers 3/4 correct, which "is good for a 24-way choice."

• Q: How is 24 computed here?
• A: There are 24 people

On "much bigger" datasets we can train on "a much smaller fraction" of the data.

Suppose we have millions of relational facts in form (A R B).

• We can train a neural net to discover a feature vector representations of the terms that allow the third term to be predicted from the first two.
• We can use the trained net to find very unlikely triples. These are good candidates for errors in the database.
• Instead of predicting third term we could use all three as input and predict the probability that the fact is correct. To do this we would need a good source of false facts.

4b - A Brief Diversion Into Cognitive Science

In cognitive science it's usually taught that there are two rival theories of a concept:

Feature Theory: a concept is a set of semantic features.

• good for explaining similarities between concepts
• convenient for analysis because then a concept is a vector of feature activities.

Structuralist Theory: the meaning of a concept lies in its relationships to other concepts.

• conceptual knowledge is best expressed as a graph
• Minsky used limitations of perceptrons as evidence against feature vectors and in favor of relational graph representations

Hinton thinks both sides are wrong, and they need not be rivals. A neural net can use vectors to construct a graph.

• In the family tree example, no "explicit" inference is required to arrive at the intuitively obvious consequences of the facts that have been explicitly learned.

We do a lot of "analogical reasoning" by just "seeing" the answer with no commonsense or intervening steps. Even when we are using explicit rules [as in math or logic], we need to "just see" which rules to apply.

Localist vs Distributed Representations of Concepts

The obvious way to implement a relational graph is to treat the neuron as a node in the graph. This won't work.

• We need many different types of relationship and connections in a neural net do not have discrete labels.
• We need ternary relationships as well as binary ones: A is between B and C.

The right way is still an open issue. Many neurons are probably used for each concept and each neuron is probably involved in many concepts: a distributed representation.

4c - The Softmax Output Function

Squared error cost function has drawbacks:

• There is almost no gradient if desired output is 1 and actual output is 0.00000001
  • it's way out on a plateau where the slope is almost exactly horizontal
  • it will take a long time to adjust, even though it's a big mistake
• If we are trying to pick between mutually exclusive classes and we know probabilities should sum to one, no way to encode that
  • there is no reason to deprive network of this information

Softmax is a different cost function applied to a group of neurons called a softmax group. It is a "soft, continuous version of the maximum function."

$z_i$ is the total input from layer below, called the logit.

$y_i$ is the output of each unit, which depends on the logits of the other units in the softmax group. In the group, the outputs all sum to one, because they are given by a formula that takes into account all of the logits of the group:

$$y_i = \frac{e^{z_i}}{\sum_{j \in group} e^{z_j}}$$

Essentially, the output yi is the zi over the sum over all zi_s in the softmax group, except where each is expressed as a power function of e. So yi is always between zero and one.

Softmax has simple output derivatives, though not that trivial to derive:

$$\frac{\delta y_i}{\delta z_i}=y_i(1-y_i)$$

Question

If $\mathbf{z} = (z_1, z_2, \ldots z_k)$ is the input to a k-way softmax unit, the output distribution is $\mathbf{y}=(y_1, y_2, \ldots y_k)$, where $y_i = \dfrac{\exp(z_i)}{\sum_j\exp(z_j)}$, which of the following statements are true?

1. The output distribution would still be the same if the input vector was cz for any positive constant c.
2. The output distribution would still be t he same if the input vector was c + z for any positive constant c.
3. Any probability distribution P over discrete states $P(x) > 0 \ \ \forall x$ can be represented as the output of a softmax unit for some inputs.
4. Each output of a softmax unit always lies in (0,1).

Work

1. If you scale z, then you change the denominator much more than the numerator, so that will change the distribution. False. Correct
2. If you add a constant to each term, that should not affect the distribution. True.
   1. Correct. Let's say we have two z's: z1=2, z2=-2. Now let's take a softmax over them: $\frac{\exp(z_1)}{\exp(z_1) + \exp(z_2)}=\frac{\exp(2)}{\exp(2)+\exp(-2)}$. If we add some positive constant c to each $z_i$ then this becomes: $\frac{\exp(2+c)}{\exp(2+c) + \exp(-2+c)}=\frac{\exp(2)\exp(c)}{(\exp(2)+\exp(-2))\exp(c)}=\frac{\exp(2)}{\exp(2)+\exp(-2)}$. Multiplying each $z_i$ by c gives: $\frac{\exp(2c)}{\exp(2c) + \exp(-2c)}=\frac{\exp(2)^c}{\exp(2)^c + \exp(-2)^c} \neq \frac{\exp(2)}{\exp(2)+\exp(-2)}$
3. I see no reason why any probability distribution over discrete states could not be represented by softmax. True. Correct
4. True. Correct

Cross-Entropy Is Cost Function To Use With Softmax

Question: if we're using a softmax group for the outputs, what's the cost function?

Answer: one that gives the negative log probability of right answer

Cross-entropy cost function for each output assumes that the for the unit under consideration, the target value is one, and all other target values for j are zero. Then take the sum of the targets times the outputs for all outputs.

$$C=-\sum_{j} t_j \log{y_j}$$

$t_j$ is the target value under consideration.

This is called the cross-entropy cost function

C has very big gradient when target value is zero and output is almost zero

• value of 0.000001 (1/M) is much better than 0.000000001 (1/B)
• cost function C has a very steep derivative when answer is very wrong
• the steepness of the derivative of the cost function with respect to the neuron's output, dC/dy balances the flatness of the derivative of the output with respect to the logit, dy/dz.

$$\frac{\delta C}{\delta z_i}=\sum_j \frac{\delta C}{\delta y_j}\frac{\delta y_j}{\delta z_i}=y_i-t_i$$

• For a given neuron i, the derivative of the cost function with respect to the logit is just the difference between the output and the target output at that neuron
• When actual target outputs are very different, that has a slope of one or minus one, and slope is never bigger than one or minus one.
• Slope never gets small until two things are pretty much the same, in other words, you're getting pretty much the right answer.

4d - Neuro-Probabilistic Language Models

We're use our understanding to hear the correct words

"We do this unconsciously when we wreck a nice beach." -> recognize speech

Standard Trigram Method

count frequencies of all triples on words in a huge corpus

$\frac{p(w_3=c \mid w_2=b, w_1=a)}{p(w_3=d \mid w_2=b, w_1=a)}=\frac{count(abc)}{count(abd)}$

• use freqs to make bets on relative prob of words given two previous words
• was state of art until recently
• cannot use much bigger context because too many possibilities to store and counts would mostly be zero
  • too many - really? 10k^3
• Dinosaur pizza ... then what?
  • "back-off" to digrams when count for trigram is too small

Trigram Limitations

example: “the cat got squashed in the garden on friday”

• should help us predict words in “the dog got flattened in the yard on monday”

does not understand similarities between ...

• cat/dog; squashed/flattened; garden/yard; friday/monday

we need to convert the words into a feature vector

Yoshua Bengio Next Word Prediction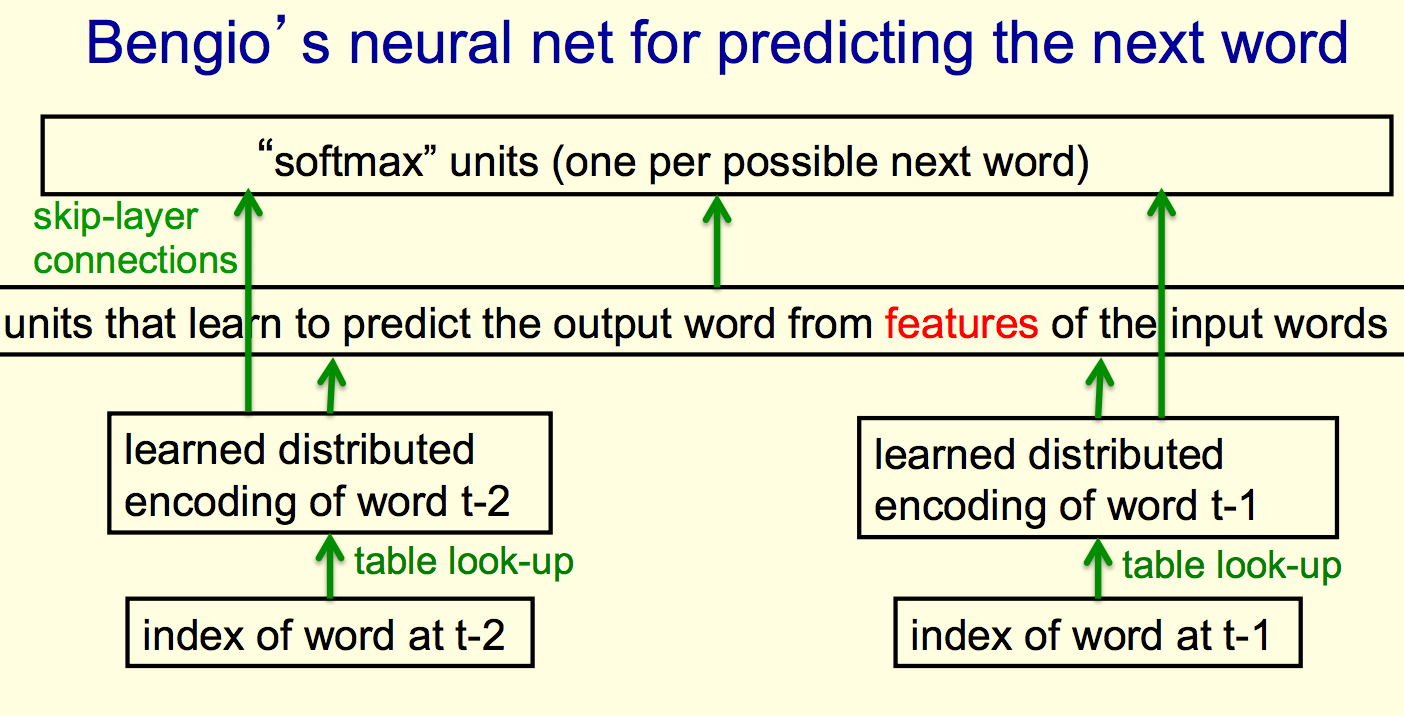

This is a similar approach to the family trees neural network mentioned earlier, but bigger and applied to a real problem.

The bottom layer, "index of a word" is a set of neurons where only one is on at a time. This is "equivalent to table look-up."

• Here it sounds like there is a one to one correlation between neurons and words
• What does it mean that only one is on at a time; is that during training, use, or both?

"You have a stored feature vector for each word, and with learning, you modify that feature vector, which is exactly equivalent to modifying the weights coming from a single active-input unit."

• Here it sounds like he's saying that there is one word per neuron, and their inputs are fed an array of n-grams.
• What algorithm determines how the feature vector is modified?
  • At the beginning of Lecture 4a he talked about backpropagation...
• By "feature vector" does he mean the context of the words activated around the current word?

You usually get "distributed representations" of a "few previous words," here shown as two, but it is typically around five.

You can then use those "distributed representations" via the hidden layer to predict "via huge softmax" what the probabilities are for all the various words that come next.

Refinement: add skip-layer connections from the input words to the output layer, since individual words can have a big impact on the next word.

• I'm not sure I understand this, but I believe it's like saying that in the case of rare digrams, the first word is all you need to determine the second word.

You put in candidate for third word, then get an output score for how good that candidate word is in the context.

• run forwards through net many times, one for each candidate.

• input context to the big hidden layer is the same for each candidate word.

Bengio's model is slightly worse at predicting the next word than Trigram, but if you combined it with Trigram, it is better than Trigram.

Question

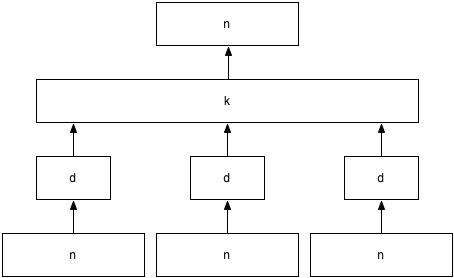
Consider the following two networks with no bias weights. The network on the left takes 3 n-length word vectors corresponding to the previous 3 words, computes 3 d-length individual word-feature embeddings and then a k-length joint hidden layer which it uses to predict the 4th word. The network on the right is comparatively simpler in that it takes the previous 3 words and uses them to predict the 4th word.

If n = 100,000, d = 1,000, and k = 10,000, which network has more parameters?

1. The network on the left
2. The network on the right

Work

This is essentially like asking what takes more memory, the trigram model, or Yoshua Bengio's model given those specific tunings.

I'm a little unclear about the definition of parameters here. Does parameters mean total inputs in the system? If there are 10k words, then there should be (10^3)^3 trigrams from which to produce the probability.

Explanation: The network on the left as 3nd + 3dk + nk parameters which comes out to 1,330,000,000 while the network on the right has 30,000,000,000 parameters, an order of magnitude more. One advantage of the neural representation is that we can get much more compact representations of our data while still making good predictions.

Follow Up: Where does the 30,000,000,000 come from?

The Problem With 100k Output Words

One problem with having a big softmax output layer is that you might have 100,000 different output weights.

There are various tenses of words, plural is different word than regular world.

As each unit in last hidden layer of net might have 100k outgoing weights.

• Then we have danger of overfitting.
  • unless we are google and have huge number of training cases.
• We could make the last hidden layer small, but then it's hard to get the 100k probabilities correct
  • small probabilities are often important.

4e - Dealing With Many Possible Outputs In Neuro-Probab. Lang. Models

Someone on the board recommended reading Minih and Hinton, 2009 for this part of the lecture

Avoiding having 100k different output units: Way 1

Serial Architecture

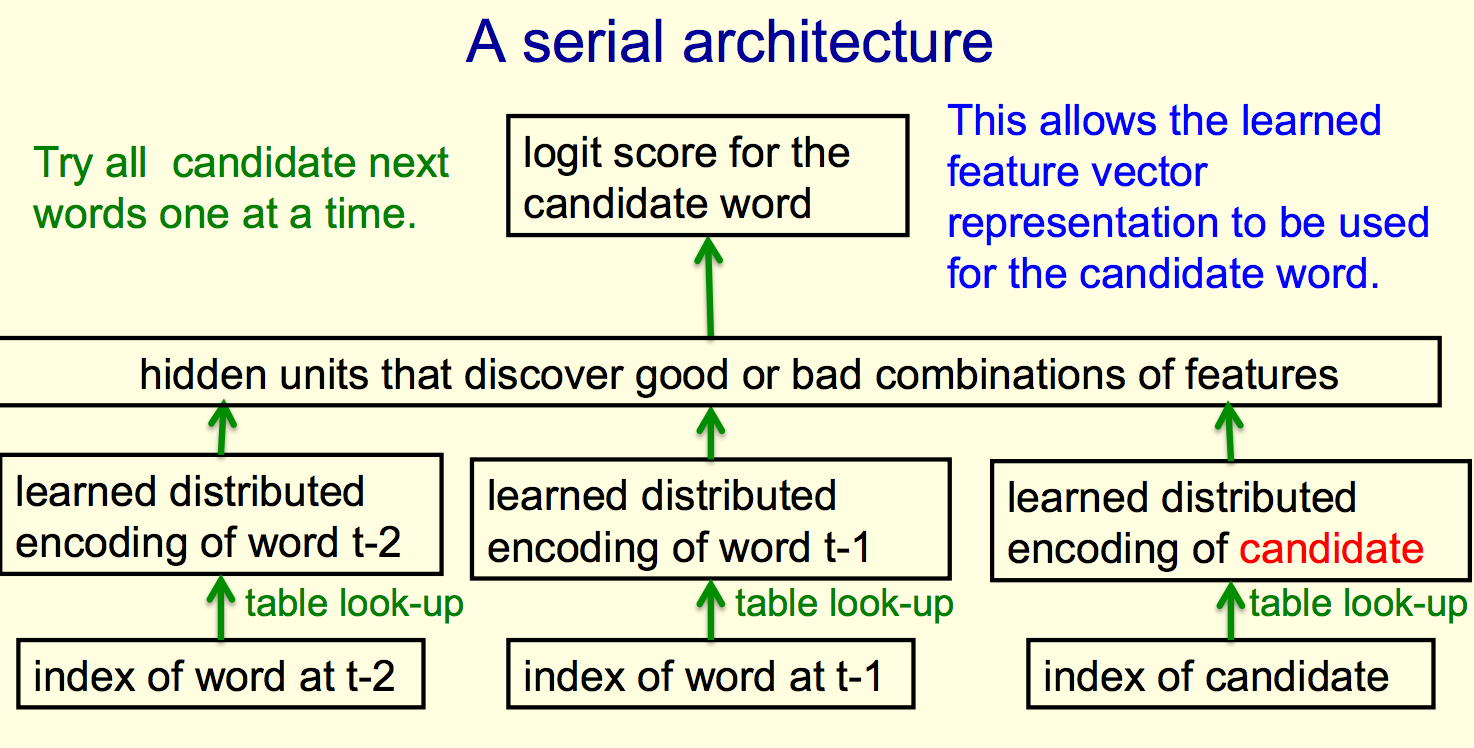Trying to predict next word or middle word of string of words.

The candidate's word index is used as part of the context sometimes and as a context later.

Put the candidate in with the its context words as before.

Go forwards through net, and then give score for how good that vector is in the net.

After computing logit score for each candidate word, use all logits in a softmax to get word probabilities.

The difference between the word probabilities and their target probabilities gives cross-entropy error derivatives. The derivatives try to raise the score of the correct candidate and lower the scores of its high-scoring rivals.

We can save time if we only use a small set of candidates suggested by some other predictor, for example, use the neural net to revise the probabilities of the words the trigram model thinks are likely (a second pass).

Avoiding having 100k different output units: Way 2

Predicting Path Through Probability Tree

Based on Minih and Hinton, 2009

Arrange all words in binary tree with words as leaves

Use previous context of previous words to generate prediction vector, v.

• Since he mentions previous context, I assume that he means this process is repeated. How do we construct the prediction vector in one context? Is it an additive process, where every time we find a word, if we find a word before it pointing to it, we add to the probability? If so, how is that done?

We compare that prediction vector with a vector that we learn for each node of the tree.

Then we compare by taking a scalar product of the prediction vector and the vector that we've learned for the node of the tree, and then apply the logistic function to that scalar product.

That will give us the probability of taking the right branch in the tree.

• This is meaning here seems to be elided.
• It's easy to see once you have a probability tree why it is useful, but it's not clear how to construct it.

It's fast at training time but slow at test time.

Simpler Way To Learn Features For Words

Collobert and Weston, 2008

Learn feature vectors for words, look at 11 words, 5 in past and 5 in future. In middle of that, either put a correct word or a random net, and then use a neural net to go high if it's the right word, and low if it's the wrong word.

What they are doing is whether the middle word is the appropriate word for the context. They trained this on ~600 million examples from English wikipedia.

Displaying learned feature vectors in a 2-D map

By displaying on 2-D map, we can get idea of quality of learned feature vectors

Multi-scale method t-sne

Easy substitutes area clustered near one another. Example Image:

Multi-scale method t-sne displays similar clusters near each other, too

• no extra supervision
• information is all in the context; some people think we learn words this way
• "She scrommed him with the frying pan" - does it mean bludgeoned or does it mean impressed him with her cooking skills?

Examples of t-sne

• matches, games, races, clubs teams, players together
• things you win together: cup, bowl, medal, prize, award
• games: rugby, soccer, baseball, sports
• places: US states at top, then cities in north america, then underneath are a lot of countries.
• adverbs: likely probably possibly perhaps
• entirely completely fully greatly
• which that whom what how whether why

4g - Quiz

Question 1

[multiple choice] The squared error cost function with n linear units is equivalent to:

1. The cross-entropy cost function with an n-way softmax unit.
2. The cross-entropy cost function with n logistic units.
3. The squared error cost function with n logistic units.
4. None of the above

Question 1 Clarification

Let's say that a network with $n$ linear output units has some weights $w$. $w$ is a matrix with $n$ columns, and $w_i$ indexes a particular column in this matrix and represents the weights from the inputs to the i-th output unit.

Suppose the target for a particular example is j (so that it belongs to class j in other words).

The squared error cost function for n linear units is given by:

$$\frac{1}{2}\sum_{i=1}^{n} (t_i-w_i^{T} x)^{2}$$

Where t is a vector of zeros except for 1 in index j.

The cross-entropy cost function for an n-way softmax unit is given by

$$-\log{(\frac{\exp(w_j^{T} x)}{\sum_{i=1}^{n} \exp(w_i^{T} x)})}$$

which is equivalent to

$$-w_j^{T}x+\log{(\sum_{i=1}^{n} \exp(w_i^{T}x))}$$

. Finally, n logistic units would compute an output of $\sigma(w_i^{T}x)=\frac{1}{1+\exp(-w_i^{T}x)}$ independently for each class i. Combined with the squared error the cost would be:

$$\frac{1}{2}\sum_{i=1}^{n} (t_i-\sigma(w_i^{T}x))^{2}$$

where again, t is a vector of zeros with a 1 at index j (assuming the true class of the example is j).

Using this same definition for t, the cross-entropy error for n logistic units would be the sum of the individual cross-entropy errors:

$$-\sum_{i=1}^{n} t_i\log(\sigma(w_i^{T}x))+(1-t_i)\log(1-\sigma(w_i^{T}x))$$

For any set of weights w, the network with n linear output units will have some cost due to the squared error cost function. The question is now asking whether we can define a new network with a set of weights $w^*$using some (possibly different) cost function such that:

a) $w^*=f(w)$ for some function $f$

b) For every input the cost we get using w in the linear network with squared error is the same cost we would get using $w^*$ in the new network with the possibly different cost function.

Question 1 Work

If we have a squared error cost function with n linear units,

1. No - for every input, the net cost we get using w in the linear network with squared error can't be equivalent to the net cost of the cross-entropy cost function with n-way softmax. For any softmax group, the output profile cannot be equivalent to a linear output profile.
2. No - linear units with squared error cost function can't produce the same output profile as logistic units with the cross-entropy cost function
3. No - linear units with squared error cost function can't produce same output profile as logistic units with squared error cost function.
4. Yes - None of the above.

Question 2

[single choice] A 2-way softmax unit (a softmax unit with 2 elements) with the cross entropy cost function is equivalent to:

1. A logistic unit with the cross-entropy cost function.
2. A 2-way softmax unit (a softmax unit with 2 elements) with the squared error cost function.
3. Two linear units with the squared error cost function
4. None of the above.

Question 2 Clarification

In a network with a logistic output, we will have a single vector of weights $w$. For a particular example with target $t$ (which is 0 or 1), the cross-entropy error is given by:

$$-t\log(\sigma(w^Tx))-(1-t)\log(1-\sigma(w^Tx))$$

where $\sigma(w^Tx)=\frac{1}{1+\exp(-w^Tx)}$.

The squared error if we use a single linear unit would be $\frac{1}{2}(t-w^{T}x)^2$.

Now notice that another way we might define t is by using a vector with 2 elements, [1,0] to indicate the first class, and [0,1] to indicate the second class. Using this definition, we can develop a new type of classification network using a softmax unit over these two classes instead. In this case, we would use a weight matrix w with two columns, where $w_i$ is the column of the $i^{th}$class and connects the inputs to the $i^{th}$ output unit.

Suppose an example belonged to class j (where j is 1 or 2 to indicate [1,0] or [0,1]). Then the cross-entropy cost for this network would be:

$$-\log(\frac{\exp(w_j^Tx)}{\exp(w_1^Tx)+\exp(w_2^Tx))})=-w_j^Tx + \log(\exp(w_1^Tx)+\exp(w_2^Tx))$$

For any set of weights w, the network with a softmax output unit over 2 classes will have some error due to the cross-entropy cost function. The question is now asking whether we can define a new network with a set of weights $w^*$ using some (possibly different) cost function such that:

a) $w^*=f(w)$ for some function f

b) For every input, the cost we get using w in the network with a softmax output unit over 2 classes and cross-entropy error is the same cost that we would get using $w^*$ in the new network with the possibly different cost function.

Question 2 Work

Cross-entropy cost $C = -\sum_jt_j\log{y_j}$ for each j in a softmax group where there is a single term t and all others are 1-t. For a 2-series, distributing the sum, computing the cost for a 2-way softmax with cross entropy, it's $-t\log{y_1}-(1-t)\log{y_2}$. Another way to say this is to realize that the output function is a function of the product of the weight vector and the input, as given above:

$-t\log(\sigma(w^Tx))-(1-t)\log(1-\sigma(w^Tx))$

Softmax output is given by $y_i = \frac{e^{z_i}}{\sum_{j \in group} e^{z_j}}=\frac{\exp(z_i)}{\sum_{j \in group} \exp(z_j)}$.

Logistic neuron output is given by $z=b+\sum_i x_iw_i$ and $y=\frac{1}{1+\exp(-z)}$

So is the cost or error of a 2-way softmax with cross-entropy equivalent to ...

1. ... A logistic unit with the cross-entropy cost function? True.
2. ... A 2-way softmax unit with the squared error cost function? False.
3. ... Two linear units with the squared error cost function? False.
4. ... None of the above? False.

Question 3

The output of a neuro-probabilistic language model is a large softmax unit and this creates problems if the vocabulary size is large. Andy claims that the following method solves this problem:

At every iteration of training, train the network to predict the current learned feature vector of the target word instead of using a softmax. Since the embedding dimensionality is typically much smaller than the vocabulary size, we don't have the problem of having many output weights any more. Which of the following are correct? Check all that apply.

1. The serialized version of the model discussed in the slides is using the current word embedding for the output word, but it's optimizing something different than what Andy is suggesting.
2. If we add in extra derivatives that change the feature vector for the target word to be more like what is predicted, it may find a trivial solution in which all words have the same feature vector.
3. In theory there's nothing wrong with Andy's idea. However, the number of learnable parameters will be so far reduced that the network no longer has sufficient learning capacity to do the task well.
4. Andy is correct. This is equivalent to the serialized version of the model discussed in the lecture.

Question 3 Work

Here is the referenced slide from this week's lecture:

1. True - the serialized version above is optimizing the lowest error on the logit score for the candidate word. This is different than optimizing for having the most correct feature vector.

2. True - if we "train the network to predict the current learned feature vector of the target word" then we may find that there are many false positives. This is because the features are always relative to the history of the target word, so if we make the features more like the targets, we might end up with many false positives. I'm not sure this is what Hinton meant by extra derivatives, though.

3. False - there is something wrong with this idea

4. False - there is something wrong with this idea

Question 4

We are given the following tree that we will use to classify a particular example x.

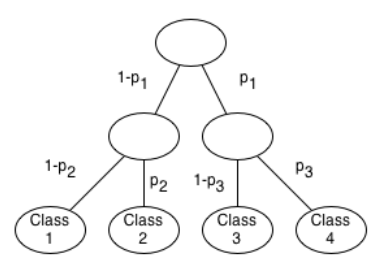
In this tree, each value indicates the probability that x will be classified as belonging to a class in the right subtree of the node at which that was computed. For example, the probability that belongs to Class 2 is $(1-p_1)*p_2$

. Recall that at training time this is a very e cient representation because we only have to consider a single branch of the tree. However, at test- time we need to look over all branches in order to determine the probabilities of each outcome.

Suppose we are not interested in obtaining the exact probability of every outcome, but instead we just want to find the class with the maximum probability. A simple heuristic is to search the tree greedily by starting at the root and choosing the branch with maximum probability at each node on our way from the root to the leaves. That is, at the root of this tree we would choose to go right if and left otherwise.

For this particular tree, what would make it more likely that these two methods (exact search and greedy search) will report the same class? [multiple choice]

1. It helps if the value of each p is close to 0 or 1
2. It helps if $p_1$is further from 0.5. It hurts if $p_2$ is further from 0.5.
3. It helps if the value of each p is close to 0.5
4. It helps if $p_1$is further from 0.5 while $p_2$ and $p_3$ are close to 0 or 1.

Question 4 Work

If you want to minimize the number of times it takes to find the right answer, decisions higher up the tree matter more than decisions deep in the tree. If earlier branches are farther from 0.5, then you have more assurance that you have made the correct decision. In a two layer path decision network like this one, the first decision is the only one you need to get correct in order to ensure you don't waste your time. Therefore #1 and #2 are the correct answers, because they are the only ones that address the need for p1 to be as far from 0.5 as possible. When p1 is close to 0.5, then it means that the remaining probabilities must be decided farther down the tree, and there are more opportunities to get it wrong.

Question 5

True or false: the neural network in the lectures that was used to predict relationships in family trees had "bottleneck" layers (layers with fewer dimensions than the input). The reason these were used was to prevent the network from memorizing the training data without learning any meaningful features for generalization.

Question 5 Work

True. This is exactly why he created a bottleneck there, to force the network to learn things other than the identities of the input people.

Question 6

In the Collobert and Weston model, the problem of learning a feature vector from a sequence of words is turned into a problem of [pick one]:

1. Learning to predict the middle word in the sequence given the words that came before and the words that came after.
2. Learning to predict the next word in an arbitrary length sequence.
3. Learning a binary classifier.
4. Learning to reconstruct the input vector.

Question 6 Work

The question was about whether a suggested middle word looked good or looked random. This question is a binary classifier (#3).

Question 7

Suppose that we have a vocabulary of 3 words, "a", "b", and "c", and we want to predict the next word in a sentence given the previous two words. Also suppose that we don't want to use feature vectors for words: we simply use the local encoding, i.e. a 3-component vector with one entry being 1 and all other two entries being 0.

In the language models that we have seen so far, each of the context words has its own dedicated section of the network, so we would encode this problem with two 3-dimensional inputs. This makes for a total of 6 dimensions; clearly, the more context words we want to include, the more input units our network must have. Here's a method that uses fewer input units:

We could instead encode the counts of each word in the context. So a context of "a a" would be encoded as input vector [2 0 0] instead of [1 0 0 1 0 0], and "b c" would be encoded as input vector [0 1 1] instead of [0 1 0 0 0 1]. Now we only need an input vector of the size of our vocabulary (3 in our case), as opposed to the size of our vocabulary times the length of the context (which makes for a total of 6 in our case). Are there any significant problems with this idea?

1. Yes: the network loses the knowledge of the location at which a context word occurs, and that is valuable knowledge.
2. Yes: even though the input has a smaller dimensionality, each entry of the input now requires more bits to encode, because it's no longer just 1 or 0. Therefore, there would be no significant advantage.
3. Yes: the neural networks shown in the course so far cannot deal with integer inputs (as opposed to binary inputs).
4. Yes: although we could encode the context in this way, we would then need a smaller bottleneck layer than we did before, thereby lowering the learning capacity of the model.

Question 7 Work

If we do this, then [1 1 0] no longer encodes "a" then "b", so there is information loss. A is the right answer.

Week 4 FAQ

1. What is the exp function mentioned in equations?

   • exp(x) calculates the value of e to the power of x. It's often used when it would make a math equation cumbersome to look at, for instance if you had exp(x)^2 it might be easier to understand than if you had two layers of powers. - tex stack exchange

2. In neural networks, what is a cost function?

   • "In artificial neural networks, the cost function [is a function] to return a number representing how well the neural network performed to map training examples to correct output." - wikipedia

   • A list of cost functions used in neural networks, alongside applications from SE: Cross Validated

3. Why does Hinton use "squared error" but also use "cross entropy cost function?" Are "error function" and "cost function" interchangeable?

   • "A loss function is part of a cost function which is a type of objective function" from SE: Cross Validated