Assignment 2 - Learning word representations
Overview
- feed mini batches of 100 training cases through forward propagation,
- use backpropagation to update weights at each layer
- the output layer is a softmax group over the vocabulary, representing discrete probabilities of a fourth word given three input words
- error function is cross-entropy
- print out the average cross-entropy error of softmax group over vocabulary units at the end of each mini batch and each 100 mini batches. This should decrease as time goes on.
Overview - Network Structure
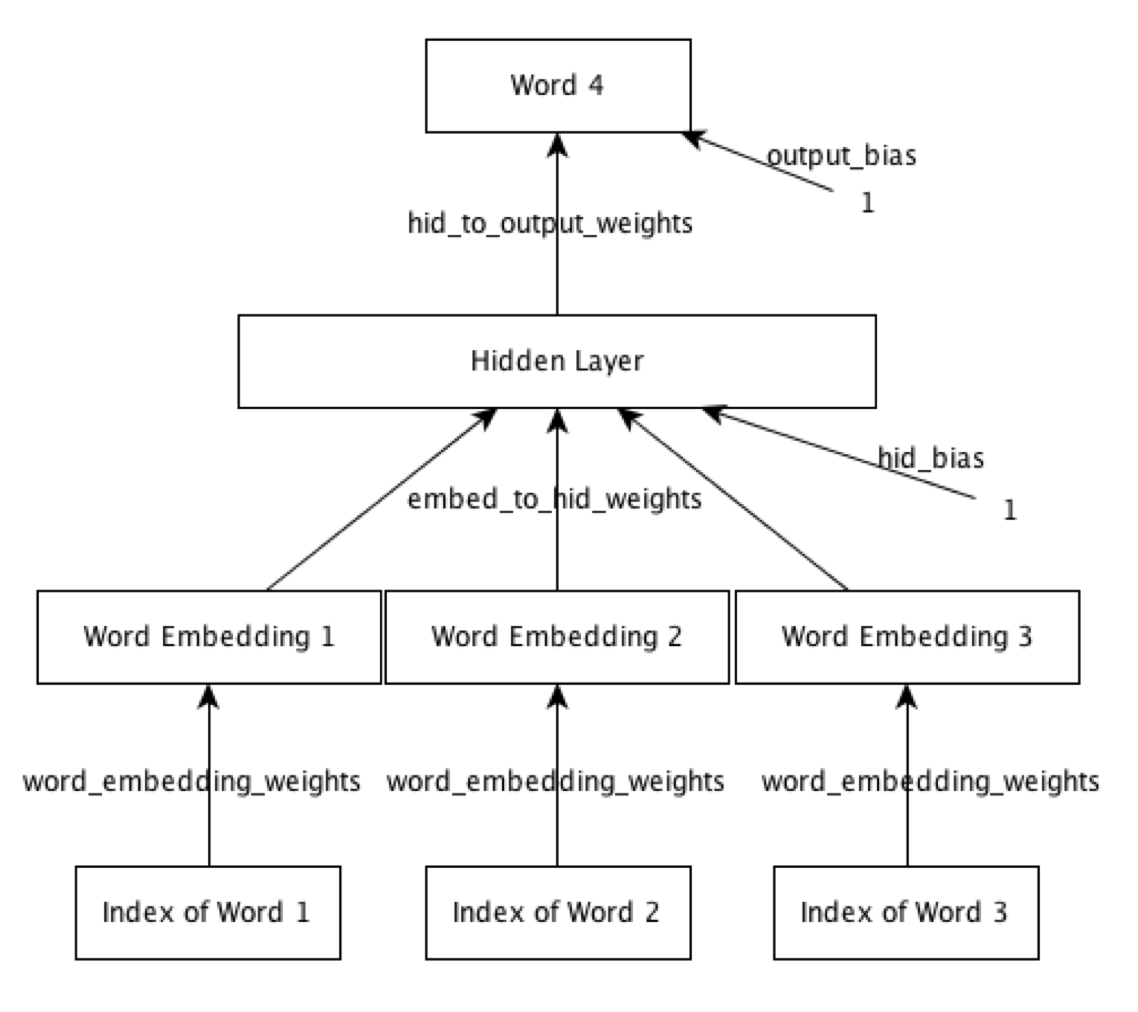
- layer 4: output layer
- description: a softmax over
vocab_size (250)units each representing a possible 4th word - input:
- data:
numhid2 (200)from hidden layer - weights:
hid_to_output_weights [] - bias:
output_bias [numhid2 (200), 1], matrix of zeros - logit:
- :
input data * input weights + input bias
- :
- data:
- output: softmax
- w.r.t logit:
- derivative w.r.t. logit:
- error: cross entropy
- : zero at non-target output, 1 at target output
- : output at jth unit
- w.r.t. output given target ouput:
- derivative w.r.t. output given target outputs:
- description: a softmax over
- hidden layer
- description:
numhid2 (200)hidden layer units connect the embedding layer to the output layer - input
- input data
- incoming weights from embedding layer are in
hid_to_output_weights- initialized with
zeros(numhid2, vocab_size);, a matrix of zeroes withnumhid2rows andvocab_sizerows. - Note that
word_embedding_weightshasvocab_sizecolumns, andhid_to_output_weightshasvocab_sizerows.
- initialized with
- bias of units captured in
hid_bias- initialized with
zeros(numhid2, 1);, a matrix withnumhid2rows and 1 column.
- initialized with
- each of the
numhid2(200) units has:numhid1(50) inputs from embedding layer- 1 output
- description:
- embedding layer
numhid1 (50)configures the number of units in the embedding layer- incoming weights from input layer are in
word_embedding_weights- initialized with
init_wt * randn(vocab_size, numhid1), a matrix of 0 +/- 0.01 with dimensions[vocab_size (250), numhid1 (50)]
- initialized with
- bias of units - unmentioned. presumably zero.
- each of the
numhid1(50) units have:- 3 inputs from input layer
- 1 output
- input layer
- consists of three word indices; it's a 3d vector of int word indices
- trained in batches of 100
- each input batch is a matrix of 3 rows and 100 columns by default
- constitutes 100 training cases of 3 ints corresponding to word indices
- bias of units - unmentioned. presumably zero.
- each of the 3 units have:
- 1 input
- 1 output
Overview - Procedure
load_data(batchsize)- comes from
./raw_sentences.txt - returns
train_input, train_target, valid_input, valid_target, test_input, test_target, vocab vocabis a column matrix of one word per row- all other vars are matrices whose contents refer to an index within
vocab - these all come from lines of
data.mat - The training set consists of 372,550 4-grams
train_inputandtrain_targetare both[4 x 372,550]matrices
- The validation and test sets have 46,568 4-grams each.
valid_input,valid_target,train_input,train_targetare each[4 x 46,568]- these variables are set up in
load_data.m - validation and test data are each from prepared data in
data.mat
- comes from
- For each epoch / training iteration:
- Define a mini-batch of 100 cases from
train_inputandtrain_target - Train network on mini-batch
- Every 100 mini-batches, compute average per-case Cross Entropy (CE) obtained on the training set during the 100 mini-batches
- Every 1000 mini-batches, run on validation set and state that Cross Entropy
- Define a mini-batch of 100 cases from
- At the end of training, run both on validation set and on test set and state cross entropy for each
File Notes
train.m before forward propagation
For each epoch and each mini-batch:
Setup input_batch, target_batch
input_batch = train_input(:, :, m);
target_batch = train_target(:, :, m);
train_inputcontains stack of training cases of (words,cases_in_batch)mis the mini-batch number we're focusing on
input_batchcontains (words,cases_in_batch) for the selected mini-batchtarget_batchalso contains (words,cases_in_batch), except it's the target output for the input batch, so it's if there areDelements incases_in_batch, it's of dimension1xD.wordshere refers to the index of the word in the vocabulary
Call forward network propagation
% FORWARD PROPAGATE.
% Compute the state of each layer in the network given the input batch
% and all weights and biases
[embedding_layer_state, hidden_layer_state, output_layer_state] = ...
fprop(input_batch, ...
word_embedding_weights, embed_to_hid_weights, ...
hid_to_output_weights, hid_bias, output_bias);
fprop.mis called, which takes as parameters:input_batchdescribed above; 3 rows for each word in training; columns are batch casesword_embedding_weights, a vector updated after each run through net- initialized to
init_wt * randn(vocab_size, numhid1); randn(vocab_size, numhid1): "Return a matrix with normally distributed random elements having zero mean and variance one. The arguments are handled the same as the arguments forrand."- returns a matrix of random values from (-1, 1) scaled to
init_wt, which is0.01by default; that way the standard deviation is 1%. numhid1 = 50; % Dimensionality of embedding space; default = 50.- each of the 50 embedded layer units store one weight for each word in the vocab
init_wtis a scalar andrandnis a matrix that is (vocab_size,50).word_embedding_weightsis a matrix where rows correspond to a single word in the vocab and columns are the weights for that word for each of the 50 embedding layer units. They are initialized to random values in a normal distribution with standard deviation of +/- 0.01 of 0.
- initialized to
embed_to_hid_weightsis initializedinit_wt * randn(numwords * numhid1, numhid2);- one row for each weight stored in
word_embedding_weights- Q: this surprises me a little bit. does this imply that we have skip layer connections?
- we shouldn't, according to the network topology picture
- Q: why isn't it one output weight for each neuron in the embedding layer?
- Q: this surprises me a little bit. does this imply that we have skip layer connections?
- one column for each unit in the hidden layer; by default there are 200 columns
- weights are initialized to random values +/- 0.01 of 0 like
word_embedding_weights
- one row for each weight stored in
hid_to_output_weightsis a 200x250 matrix that was initialized withinit_wt * randn(numhid2, vocab_size), so it has random values +/- 0.01 of 0 in the dimensions of 200x250, since by default there are 200 hidden units.hid_biasis initialized tozeros(numhid2, 1);- it's a vector storing a bias for each of the 200 hidden units, by default 0
output_biasis initialized tozeros(vocab_size, 1);- it's a vector storing a bias for each of the words in the vocab, by default 0
fprop.m forward propagation
- Compute State of Word Embedding Layer
embedding_layer_state = reshape(... word_embedding_weights(reshape(input_batch, 1, []),:)',... numhid1 * numwords, []);reshape(input_batch, 1, [])- reshape the 3x100 input batch into a 1x300 column matrix so all the words are in a row
word_embedding_weights(reshape(input_batch, 1, []),:)word_embedding_weightsis a matrix where rows correspond to one word in vocab and columns are the weights for that word for each of 50 embedded feature representation units- construct a new matrix by repeatedly selecting and stacking rows from
word_embedding_weights - for each of 300 word indexes in test batch, output the row of
50 weights from
word_embedding_weightscorresponding to that word - we end up with a 300x50 matrix of all the words in the input batch matched with all the weights for each of 50 units
word_embedding_weights(reshape(input_batch, 1, []),:)'- note the
'at the end - transpose the matrix we got in #2, so now it's 50 rows of weights for 300 columns of input words in this batch
- note the
embedding_layer_state = reshape(... word_embedding_weights(reshape(input_batch, 1, []),:)',... numhid1 * numwords, []);numwords(3) is num words in training batch, not to be confused withvocab_size(250):[numwords, batchsize] = size(input_batch); [vocab_size, numhid1] = size(word_embedding_weights);numwordsis the number of input words in a single training case: 3
- take the output from #3, which is 50 rows of weights for 300 columns of words, and reshape it into a row matrix
- the reshaped matrix has
numhid1 (50) * numwords (3) = 150rows - it's reshaped by stacking three columns from #3 into one row over and over
- why? because there are three training cases.
embedding_layer_stateis a 150x100 matrix where rows are 150 weights and columns are training cases consisting of three words at fifty weights per word = 150.
size(embedding_layer_state)is 150x100 (using default batch size of 100)
COMPUTE STATE OF HIDDEN LAYERCompute inputs to hidden unitsinputs_to_hidden_units = embed_to_hid_weights' * embedding_layer_state + ... repmat(hid_bias, 1, batchsize);embed_to_hid_weightsis supplied tofprop- initialized to:
zeros(numwords * numhid1, numhid2)=zeros(3 * 50, 200)= matrix of zeros that's 150 rows by 200 columns.- there's a data point mapping each weight in the embedding layer to a hidden node
- initialized to:
- transposition
embed_to_hid_weights'is 200 rows by 150 columns, so rows are hidden layer nodes and columns are embedding layer nodes, and values are the weights on the connections coming into the hidden layer from the embedding layer embed_to_hid_weights'(200x150) byembedding_layer_state(150x100)size(embed_to_hid_weights' * embedding_layer_state)is 200x100-
- "Form a block matrix of size m by n, with a copy of matrix A as each element."
- "If n is not specified, form an m by m block matrix. For copying along more than two dimensions, specify the number of times to copy across each dimension m, n, p, …, in a vector in the second argument."
- it sounds like
repmatcreates a tensor by repeating a matrix inside its cells?
octave:67> A=2; octave:68> repmat(A,2,3) ans = 2 2 2 2 2 2 octave:69> A = [1, 2]; octave:70> repmat(A, 2, 3) ans = 1 2 1 2 1 2 1 2 1 2 1 2 octave:71> A = [1; 2]; octave:72> repmat(A, 2, 3) ans = 1 1 1 2 2 2 1 1 1 2 2 2- From the gnu docs description, I thought it was embedding a dimension inside each cell, but that's incorrect. It's just using the first parameter as the template for the 2d matrix and repeating it a number of rows and columns according to the 2nd and 3rd parameters
repmat(hid_bias, 1, batchsize)- The hidden layer bias is initialized to
zeros(numhid2, 1), which isnumhid2(200) rows by 1 column of zeroes - We're taking a 200x1 matrix of zeroes and repeating it only one time vertically
but repeating it
batchsize(100) times horizontally, so we have a matrix that is 200x100. The rows are hidden units and the columns are test cases, and the values are the biases of each hidden layer unit.
- The hidden layer bias is initialized to
inputs_to_hidden_unitscould just as easily have beenembedded_layer_outputs.- it's a computation of multiplying embedded weights by embedded inputs and adding the biases; the embedding layer is just simple linear neurons.
inputs_to_hidden_unitsdimensions are200x100hidden units by training cases, where each value is the logit of the activation function
% Apply logistic activation function.hidden_layer_state = 1 ./ (1 + exp(-inputs_to_hidden_units));x ./ y: "Element-by-element right division"You cannot use / to divide two matrices element-wise, since / and \ are reserved for left and right matrix "division". Instead, you must use the ./ function: octave:6> x = [1, 2, 3]; y = [5, 6, 2]; y./x 5.00000 3.00000 0.66667 octave:7> 1 ./ x 1.00000 0.50000 0.33333- Q: why is the operation
./called "right division?"
- Here we're implementing the logistic activation function:
- this is already computed in
inputs_to_hidden_units
- this is already computed in
- this is
1 ./ (1 + exp(-inputs_to_hidden_units))
- this is
- In Octave, we can do this on a matrix variable end up with a matrix, and the equation looks just like we did it on one unit
hidden_layer_statethen contains the outputs of the hidden layer units; it's output is also 200x100 hidden layer units by 100 training cases in batch
%% COMPUTE STATE OF OUTPUT LAYER.% Compute inputs to softmax.inputs_to_softmax = hid_to_output_weights' * hidden_layer_state + repmat(output_bias, 1, batchsize);hid_to_output_weightswas passed as an argument tofprop. It's anumhid2 X vocab_size(200, 250) matrix where where the datapoints are the weights of the connections between thenumhid2(200) hidden layer units and thevocab_size(250) output units. It was initialized toinit_wt * randn(numhid2, vocab_size), so at the start its weights are 0 +/- 0.01 random values.hid_to_output_weights' * hidden_layer_stateis 250x200 * 200x100 = 250x100 matrix representing the weighted sum of the inputs from the hidden layer for the output layer unit logits.repmat(output_bias, 1, batchsize)is the bias for output layer unit logits.inputs_to_softmaxisvocab size (250) X batch size (200)and contains output layer logits
% Subtract maximum.- "Remember that adding or subtracting the same constant from each input to a softmax unit does not affect the outputs. Here we are subtracting maximum to make all inputs <= 0. This prevents overflows when computing their exponents."
inputs_to_softmax = inputs_to_softmax - repmat(max(inputs_to_softmax), vocab_size, 1);- Here we are subtracting the same constant from all logits to make all of them <= 0
- the claim is that this prevents overflows when computing their exponents
- Softmax output:
- since the inputs are connected to the exponent, Hinton makes it sound like there is a risk of buffer overflow if the inputs are big. This might be just a performance optimization or something he is used to from working with production data.
% Compute exp.output_layer_state = exp(inputs_to_softmax);- first, we get the numerator
% Normalize to get probability distribution.- now that we have the softmax numerator, we can get the denominator
output_layer_state = output_layer_state ./ repmat(... sum(output_layer_state, 1), vocab_size, 1);sum(output_layer_state, 1)- in the softmax equation, the denominator is the sum of all the logits
output_layer_statehas dimensionsvocab_size (250) X batch_size (100)- sum with 1 as the second parameter sums along columns / training batches
- we get a 1 x 100 matrix out, where each column is the sum across the vocab
- of all the output logits
repmat(sum(output_layer_state, 1), vocab_size, 1)- Here, we repeat the 1x100 matrix
vocab_size (250)times so we end up with a250x100matrix where in each column / training case all of the values are the same, equal to the sum of the logits for that training case.
- Here, we repeat the 1x100 matrix
output_layer_stateends up containing the outputs of the 250 words, each with a probability of that word
fpropreturnsembedding_layer_state,hidden_layer_state,output_layer_stateembedding_layer_state: "State of units in the embedding layer as a matrix of sizenumhid1*numwords X batchsize"- each of the
numhid1units (50) in the embedding layer hasnumwords(3) weights for each of thebatchsize(100) training cases
- each of the
hidden_layer_state: "State of units in the hidden layer as a matrix of sizenumhid2 X batchsize"- one row for each hidden layer unit
- one column for each training case in the mini-batch
- values are the output of the hidden layer units
output_layer_state: "State of units in the output layer as a matrix of sizevocab_size X batchsize"- one row for each word in the vocabulary
- one column for each training case in mini-batch
- values are the discrete proabilities of each word in the vocab; the output of the activation function
train.m after forward propagation
Compute Derivative
% COMPUTE DERIVATIVE.
%% Expand the target to a sparse 1-of-K vector.
expanded_target_batch = expansion_matrix(:, target_batch);
%% Compute derivative of cross-entropy loss function.
error_deriv = output_layer_state - expanded_target_batch;
- this all comes from lecture 4, where we talked about the derivative of the Cost w.r.t. the logit , which is for each .
expanded_target_batch = expansion_matrix(:, target_batch);target_batchis[1x100]; an index of a word for the target of each training case in the batchexpansion_matrixis initialized toeye(vocab_size), which is avocab_sizesquare identity matrix.expansion_matrix(:, target_batch)will return a matrix composed by going through the word indexes intarget_batchand for each column, outputting the column fromexpansion_matrixat that word index- this ends up producing a column for each column in
target_batch - each column has a 1 in the row whose index was formerly stored in
target_branchat that index
- this ends up producing a column for each column in
size(expanded_target_batch) is 250 x 100- example: if I have a set of words ["a", "b", "c"], and then
I make a
expansion_matrixidentity:
then if I have a batch of 5 training answers corresponding to indexes in the vocabulary:1 0 0 0 1 0 0 0 1target_batch = [1, 3, 2, 2, 1], then if I doexpansion_matrix(:, target_batch), I will getexpanded_target_batch:
then this1 0 0 0 1 0 0 1 1 0 0 1 0 0 0expanded_target_batchis what we need to subtract from the real output to find out how "off" the output was during this batch for each case
error_deriv = output_layer_state - expanded_target_batch;output_layer_stateis[vocab_size (250), batchsize (100)]- for each unit in the output layer, find the difference with the target output
error_deriv = output_layer_state - expanded_target_batch;- here, we're using the fact that .
- it's the change of cost/error respect to the logit of an output unit
- from lecture 4 slide, "Cross-entropy: the right cost function to use with softmax"
- here, we're using the fact that .
Measure Loss Function
% MEASURE LOSS FUNCTION.
CE = -sum(sum(...
expanded_target_batch .* log(output_layer_state + tiny))) / batchsize;
trainset_CE = trainset_CE + (CE - trainset_CE) / m;
count = count + 1;
this_chunk_CE = this_chunk_CE + (CE - this_chunk_CE) / count;
fprintf(1, '\rBatch %d Train CE %.3f', m, this_chunk_CE);
if mod(m, show_training_CE_after) == 0
fprintf(1, '\n');
count = 0;
this_chunk_CE = 0;
end
CE = -sum(sum(expanded_target_batch .* log(output_layer_state + tiny))) / batchsize;tinyis initialized toexp(-30)log(x)computes the log of x for all xlog(output_layer_state + tiny)gives avocab_size x batch_size = 250x100matrix where each element islog(state_for_unit + tiny).- we're talking about the output layer softmax here
- in octave
.*means element by element multiplication, soexpanded_target_batch .* log(output_layer_state + tiny)then gives a matrix produced by multiplyingexpanded_target_batch__{ij} * log(output_layer_state + tiny)__{ij}.- Zeroes in the expanded targets eliminate the effect of the output layer state, and the one output layer unit that is supposed to be successful is the one lets output layer state "speak" at that training case
- We get a 250x100 matrix, where in each of 100 columns, at most one row's value is non-zero.
-sum(sum(...: seesum(x)"Sum of elements along dimension dim. If dim is omitted, it defaults to the first non-singleton dimension."- sum defaults to "column-wise sum"
example:
octave:75> A = [1,2,3; 4,5,6; 7,8,9] octave:76> sum(A) ans = 12 15 18 octave:77> -sum(sum(A)) ans = -45
- For
m=1I getCE = 5.5215. - The loss function is cross entropy:
- lecture 4 slide, "Cross-entropy: the right cost function to use with softmax"
- in this case, the error is the negative log of the output at the target unit, since the output units form a softmax group
- Here we've computed it for a batch, so that's why it's divided by the batch size; we essentially have one portion of the cost function computed at each batch
trainset_CE = trainset_CE + (CE - trainset_CE) / m;trainset_CE: the cross entropy for the whole training set across all batches. Reset to zero at the beginning of an epoch.- we're computing the cumulative moving average of the cross entropy
count = count + 1; this_chunk_CE = this_chunk_CE + (CE - this_chunk_CE) / count; fprintf(1, '\rBatch %d Train CE %.3f', m, this_chunk_CE); if mod(m, show_training_CE_after) == 0 fprintf(1, '\n'); count = 0; this_chunk_CE = 0; end- this code prints the Cross Entropy "in progress" every 100 batches
Back Propagate - Output Layer
% BACK PROPAGATE.
%% OUTPUT LAYER.
hid_to_output_weights_gradient = hidden_layer_state * error_deriv';
output_bias_gradient = sum(error_deriv, 2);
back_propagated_deriv_1 = (hid_to_output_weights * error_deriv) .* hidden_layer_state .* (1 - hidden_layer_state);
hid_to_output_weights_gradient = hidden_layer_state * error_deriv';error_derivholdsoutput_layer_state - expanded_target_batch, a matrix of 250x100error_deriv'is the transpose, so a matrix of 100x250
hidden_layer_stateholds[250x100], where rows are words and cols are training cases in batch- so
hid_to_output_weights_gradientis regular matrix multiplication of the two.
output_bias_gradient = sum(error_deriv, 2);error_derivis 250x100, which is the rate of change of the loss func for 250 words x 100 training casesA = [1, 2; 3, 4]; sum(A, 2)gives:
so this means that3 7sum(error_deriv, 2)should give a row matrix where each row contains the sum of the error derivatives for that word in the mini batch. This is what is inoutput_bias_gradient
back_propagated_deriv_1 = (hid_to_output_weights * error_deriv) .* hidden_layer_state .* (1 - hidden_layer_state);(hid_to_output_weights * error_deriv)hid_to_output_weightsis a 200x250 rand 0 +/- 0.01 matrix initially- mult by error_deriv, we get 200x250 * 250x100 = 200x100 matrix
- we can understand this line if we go to lec3 slide "Backpropagating dE/dy"
(hid_to_output_weights * error_deriv)ishidden_layer_state .* (1 - hidden_layer_state);is
Back Propagate - Hidden Layer
%% HIDDEN LAYER.
embed_to_hid_weights_gradient = embedding_layer_state * back_propagated_deriv_1';
hid_bias_gradient = sum(back_propagated_deriv_1, 2);
back_propagated_deriv_2 = embed_to_hid_weights * back_propagated_deriv_1;
embed_to_hid_weights_gradient = embedding_layer_state * back_propagated_deriv_1';
Instructions
In this assignment, you will design a neural net language model that will learn to predict the next word, given previous three words.
The data set consists of 4-grams (A 4-gram is a sequence of 4 adjacent words in a sentence). These 4-grams were extracted from a large collection of text. The 4-grams are chosen so that all the words involved come from a small vocabulary of 250 words. Note that for the purposes of this assignment special characters such as commas, full-stops, parentheses etc are also considered words. The training set consists of 372,550 4-grams. The validation and test sets have 46,568 4-grams each.
GETTING STARTED
Look at the file raw_sentences.txt. It contains the raw sentences from which these 4-grams were extracted. Take a look at the kind of sentences we are dealing with here. They are fairly simple ones.
To load the data set, go to an octave terminal and cd to the directory where the downloaded data is located. Type
> load data.mat
This will load a struct called 'data' with 4 fields in it. You can see them by typing
> fieldnames(data)
'data.vocab' contains the vocabulary of 250 words. Training, validation and test sets are in 'data.trainData', 'data.validData' and 'data.testData' respectively. To see the list of words in the vocabulary, type -
> data.vocab
'data.trainData' is a matrix of 4x372550 rows vs columns. This means there are 372550 training cases and 4 words per training case. Each entry is an integer that is the index of a word in the vocabulary. So each column represents a sequence of 4 words. 'data.validData' and 'data.testData' are also similar. They contain 46,568 4-grams each. All three need to be separated into inputs and targets and the training set needs to be split into mini-batches. The file load_data.m provides code for doing that. To run it type:
>[train_x, train_t, valid_x, valid_t, test_x, test_t, vocab] = load_data(100);
Apparently Octave has destructuring. We get load_data by being in the same directory as
load_data.m, whose sole contents is the function that is run. After this is run, train_t is a variable in the space that calledload_data.Reading through
load_data.m, the function is terminated with theendkeyword. In octave, instead of areturnstatement, when declaring the function, the signature declares the names of the variables that should be returned. These are the variables destructured in the call listed here.There are several octave system functions called in this function. They are not imported via any syntax that I can see; instead, they are assumed to be in scope:
size(data.trainData, 2): size returns "a row vector with the size (number of elements) of each dimension for the object a insize(a). When given a second argument, dim, return the size of the corresponding dimension." So here, given a 4x372550 matrix,size(data.trainData, 1) -> 4andsize(data.TrainData, 2) -> 372550.
train_input = reshape(data.trainData(1:D, 1:N * M), D, N, M);: reshapeBuilt-in Function: reshape (A, m, n, …)- "Return a matrix with the specified dimensions (m, n, …) whose elements are taken from the matrix A."Dhere issize(data.trainData, 1)-1, which is3.Nwas passed as the batch size, andMis the number of batches in the columns, which is 3725. SoN*Mis 372500.data.trainData(1:D, 1:N * M)selects rows 1-3 and columns 1-372500. Note here that a range specifier of all values from 1:D (here: 3) is passed to the first parameter to select. Then we "reshape" that intoDxNxM = 3x100x3725. I assume that it goes in columns then rows when reshaping. This is what determines the vartrain_input.
This will load the data, separate it into inputs and target, and make mini-batches of size 100 for the training set.
train.m implements the function that trains a neural net language model.
To run the training, execute the following -
> model = train(1);
trainmakes a call toload_data.randn"Return a matrix with normally distributed random elements having zero mean and variance one. The arguments are handled the same as the arguments for rand."zeros"Return a matrix or N-dimensional array whose elements are all 0."eye"Return an identity matrix. If invoked with a single scalar argument n, return a square NxN identity matrix."exp"Compute e^x for each element of x."fprintf"This function is equivalent to printf, except that the output is written to the file descriptor fid instead of stdout. printf: Print optional arguments under the control of the template string template to the stream stdout and return the number of characters printed."
This will train the model for one epoch (one pass through the training set).
Currently, the training is not implemented and the cross entropy will not
decrease. You have to fill in parts of the code in fprop.m and train.m.
fprop.mcontains the forward propagation function.
Once the code is correctly filled-in, you will see that the cross entropy starts decreasing. At this point, try changing the hyperparameters (number of epochs, number of hidden units, learning rates, momentum, etc) and see what effect that has on the training and validation cross entropy. The questions in the assignment will ask you try out specific values of these.
The training method will output a 'model' (a struct containing weights, biases and a list of words). Now it's time to play around with the learned model and answer the questions in the assignment.
DESCRIPTION OF THE NETWORK
The network consists of an input layer, embedding layer, hidden layer and output
layer. The input layer consists of three word indices. The same
word_embedding_weights are used to map each index to a distributed feature
representation. These mapped features constitute the embedding layer. This layer
is connected to the hidden layer, which in turn is connected to the output
layer. The output layer is a softmax over the 250 words.
THINGS YOU SEE WHEN THE MODEL IS TRAINING
As the model trains it prints out some numbers that tell you how well the training is going.
OUTPUT:
octave:18> model = train(1);
Epoch 1
Batch 100 Train CE 5.521
Batch 200 Train CE 5.521
Batch 300 Train CE 5.521
...
Running validation ... Validation CE 5.521
Batch 1100 Train CE 5.521
Batch 1200 Train CE 5.521
Batch 1300 Train CE 5.521
...
Average Training CE 5.521
Finished Training.
Final Training CE 5.521
Final Validation CE 5.521
Final Test CE 5.521
Training took 32.49 seconds
- The model shows the average per-case cross entropy (CE) obtained on the training set. The average CE is computed every 100 mini-batches. The average CE over the entire training set is reported at the end of every epoch.
- After every 1000 mini-batches of training, the model is run on the validation set. Recall, that the validation set consists of data that is not used for training. It is used to see how well the model does on unseen data. The cross entropy on validation set is reported.
- At the end of training, the model is run both on the validation set and on the test set and the cross entropy on both is reported.
You are welcome to change these numbers (100 and 1000) to see the CE's more frequently if you want to.
SOME USEFUL FUNCTIONS
These functions are meant to be used for analyzing the model after the training is done.
display_nearest_words.m: This method will display the words closest to a given word in the word representation space.word_distance.m: This method will compute the distance between two given words.predict_next_word.m: This method will produce some predictions for the next word given 3 previous words.
Take a look at the documentation inside these functions to see how to use them.
THINGS TO TRY
Choose some words from the vocabulary and make a list. Find the words that the model thinks are close to words in this list (for example, find the words closest to 'companies', 'president', 'day', 'could', etc). Do the outputs make sense?
Pick three words from the vocabulary that go well together (for example, 'government of united', 'city of new', 'life in the', 'he is the' etc). Use the model to predict the next word. Does the model give sensible predictions?
Which words would you expect to be closer together than others? For example, 'he' should be closer to 'she' than to 'federal', or 'companies' should be closer to 'business' than 'political'. Find the distances using the model. Do the distances that the model predicts make sense?
You are welcome to try other things with this model and post any interesting observations on the forums!